A computational critique of a computational critique of computational critique.
Critical Inquiry has posted an article by Nan Da offering a critique of some subset of digital humanities that she calls “Computational Literary Studies,” or CLS. The premise of the article is to demonstrate the poverty of the field by showing that the new structure of CLS is easily dismantled by the master’s own tools. It appears to have succeeded enough at gaining attention that it clearly does some kind of work far outsize to the merits of the article itself.
The piece is not a useful contribution; it’s a magic trick that relies on the inattention or ignorance of its readers. While it pretends to demystify computation for literary among literary critics, it in fact does exactly the opposite; it operates through a series of feints and misdirections that repeatedly misstates the plain text of other scholars–in both literature and statistics–says, and what the statistical work she herself has done is. The article is predicated on an lack of statistical sophistication by the readers of Critical Inquiry.
The “computational” aspect of Da’s case is twofold:
-
It asserts that actually existing CLS is ridden with statistical errors that could be easily corrected, and claims to have performed replications.
-
It offers that in other areas–science and industry–computational methods are being deployed perfectly and appropriately; but that sadly, such methods can not be applied in literary studies because they have demonstrably demonstrated only absurditites and tautologies.
I do not believe it would be possible to write an article that defends both of these points. If existing pieces are so heavily flawed, then we probably don’t know the limits of the knowable. If, on the other hand¸ we’re able to tell that CLS will never produce useful results for literature, it would probably only be because the existing literature give us some sense of what’s possible.
But together–and this is where the appeal comes from–they break some fresh ground in the genre of anti-digital-humanities polemic. To straightforwardly attack the cultural authority of numbers has become increasingly problematic in the past few years. The hegemony of STEM has increased inside the university, making the gambit more instutionally dangerous; and at the same time, humanists have come to realize there may be forces in the world yet more sinister than scientists. The rhetorical tools you can deploy against positivism are strong, but they risk appearing to make it seem–say–that maybe we shouldn’t listen to climate scientists. So Da’s piece posits that everyone else is using numbers right–but also holds out that the exercise in replication and methodological analysis (a good thing) proffered here don’t actually hold the way out for better resource.
Da moves past anti-positivism into something fresh– call it computational NIMBYism. Rather than pooh-pooh statistical reasoning, she elevates it by incanting the language of quantification against itself. Far more than anyone I’ve seen in any humanities article, she asserts that scientists do something arcane, powerful, and true. But she returns from this promised land with hard-won truths for literary critics; its computationalists are false prophets engaged in a cargo-cult version of data science, and the true religion has nothing to say for literary scholars.
The response the article engenders.
A careful effort to replicate published articles is necessary. Fortunately, it is also something that happens, albeit not as much as might be useful. I expansively discussed the concerns Da raises about topic modeling across time in Underwood and Goldstone’s work in 2013.[@schmidt_words_2013] Their response is explicitly contained within the paper Da read. The final footnote in Ted Underwood’s new book raises precisely the same questions about the way that a Stanford Literary Lab pamphlets use of bigram entropy as a distinguishing measure. ^[For the record, I myself made a quick check using yet another measure of entropy, compressibility; I’m inclined to think Da is right that there is a fundamental error Stanford’s bigram calculations.]
But this isn’t that article. The computational evidence deployed here–the thing that tries to make this piece stand out–is striking in its sloppiness even compared to the works it pretends to debunk. Perhaps the whole piece is intended as a parody of what can slide into top literary journals nowadays. (It is indeed the case that Critical Inquiry will allow you to publish with terribly inadequate code appendices and reviewers incompetent to assess the validity of your work.) But it certainly does not show that good statistics can obliterate the bad statistics that are widespread. Instead, the most it could do is demonstrate that the literary profession is as easily bamboozled by numbers as Da says.
This tension of the two goals evident in the first piece of the set, on a Ted Underwood piece on genre classification. She at once claims a simple correction–
Underwood should train his model on pre-1941 detective fiction (A) as compared to pre-1941 random stew and post-1941 detective fiction (B) as compared to post-1941 random stew, instead of one random stew for both, to rule out the possibility that the difference between A and B is not broadly descriptive of a larger trend (since all literature might be changed after 1941).
and that Underwood uses methods that could never find differences between genres.
It is true that Underwood does use methods inadequate to prove there is no difference in detective fiction pre and post-1930. (Her use of the year “1941” is a mistake–it seems to stem from confusing the date of one of Underwood’s sources with the year he chose for a testing cutoff). This is an absurdly high bar–of course something changed, if only the existence of words like ‘television’ and ‘databases.’ Underwood says as much. The actual article is caught up in a more interesting discussion of the comparative stability of genres. The core argument is not, as Da says, that genres have been “more or less consistent from the 1820s to the present,” but that detective fiction, the gothic, and science fiction–specifically– show different patterns, with detective fiction being a far more coherent pattern than the gothic novel. By focusing only detective work, she’s missing the entire argument of the article.
That this doesn’t merit correction or retraction is depressing.
I don’t know what Underwood used to train. But if he did allow the ‘random stew’ to contain both pre- and post-1930 work that would make the performance of his model more remarkable, not less–it would indicate that it was correctly tagging Elmore Leonard (say) novels as detectives even though they use words like “fax” or “polaroid” it had previously seen in the post-1930 set.
Where Da’s method really shines, though, is in the random statistical vocabulary she brings to bear.
All that Underwood has shown in using word frequency homogeneity to differentiate detective fiction from random fiction is that the difference between pre- and post-1941 detective fiction is not as significant as its difference from random fiction. This does not mean that the same method can capture the difference between different types of detective fiction. After all, statistics automatically assumes that 95 percent of the time there is no difference and that only 5 percent of the time there is a difference. That is what it means to look for p-value less than 0.05. Think of it this way: if everyone can agree that something is changing—even Underwood concedes that genres evolve—but you have devised one way that concludes that it does not, it does not necessarily mean that you have found something.
In the first specific critique, the article talks about 95% p-values in the following way: “statistics automatically assumes that 95 percent of the time there is no difference and that only 5 percent of the time there is a difference. That is what it means to look for p-value less than 0.05.”
To look for a p-value under 0.05 is to look for a pattern that would only occur 5% of the time as a result of random variation. It’s not a great threshold. But Underwood’s paper does not rely on them.
So let’s take a look at how well the statistical claims here hold up: is the debunking useful?
Jockers and Kiriloff on Gender
Da’s critique of Underwood relies mostly on failures of reading. The next section, on work by Matthew Jockers and Gabi Kirilloff, showcases the way her piece rests rhetorically on the innumeracy of her readership. Her critique of Jockers and Kiriloff is, as she says, that they “present a statistical no-result finding as a finding.”
In order to do so, she swamps her readers with a blizzard of statistical language that she can justifiably assume will sound plausible to the readers of Critical Inquiry. Her promise is that she will offer “a clear explanation of the computational work that CLS actually does” (605). In her two paragraphs on Jockers and Kiriloff, she tosses out the following observations:
- “Let us say that you are measuring the overlap of features between two sets of data using a standard 5 percent confidence level; out of n possible shared features, 0.05n will automatically be significant.”
- “In good statistical work, the burden to show difference within naturally occurring differences (‘diff in diff’) is extremely high.”
- “This paper does not perform a bootstrap, which means the literary-historical suggestions that follow this genre classification do not stand.”
- “Practitioners have to apply the Bonferroni Correction to conventional statistical thresholds of significance used for data mining.”
And so on. This blizzard of terminology establishes for the innumerate reader that they finally have an expert who will debunk statistics for them, while freeing them of the burdensome requirement to think for themselves.
But much of this is word salad; what stands is unimportant. The claim that 5% of features “will automatically be significant” seems to approach the claim that she has already had to retract: that “statistics automatically assumes that 95 percent of the time there is no difference and that only 5 percent of the time there is a difference. That is what it means to look for p-value less than 0.05.” ‘Diff in diff’ is indeed an important tool, but it’s not about whether testing whether two distributions are different from each other; it’s about testing whether a post-treatment experimental group (like recipients of experimental chemotherapy, or counties that received Gates foundation grants) saw a significant time series change. Bootstrap resampling to generate confidence intervals can be useful, but to randomly invoke it, as here, is about as sophisticated as demanding that every article, regardless of content, take a transnational approach.
To say that significance testing should apply the Bonferroni correction is not nonsense. But neither is it something that Da does. As with her discussion of Underwood, the exercise relies on coming up with a straw man description of the claim of the article, and then rejecting that. Da focuses mostly on the question of whether there are statistically significant differences in gendered use of verbs. Jockers and Kiriloff use the method of nearest shrunken centroids as input into their model for a variety of reasons having to do with model interpretability. 1
But Jockers and Kiriloff’s findings are significant at the level that Da suggests, and it is Da’s work that is truly sloppy. In the appendix, she publishes a comparison that obviously mislabels its bins (it claims that her replication found the “she killed” and “he wept” are gender stereotypes, rather than the opposite). If the goal is simply to find which words show strong gendered patterns of usage, it’s unclear why she would choose a different statistical method. In the appendix, claims to have performed a replication and found that “Overall, the percentage differences between these top most correlated verbs for each gender was very low (0.031% to 0.307%) meaning that while a difference can be found, male/female is not very differentiated from one another if we look at verbs.” I have no idea what statistics she is reporting here–although she has a github repository online, it appears not to contain any of the code used to generate these tables. ^[I base this partly because the appendix says it uses the “SpaCy” packages for results, but none of her online code imports that package.]
But while Da’s method is obscure, I am confident that the interpretation any reader would take from this– that Jockers and Kiriloff report statistically inflated claims of difference– is incorrect. A simple way to test the robustness here is just to apply a Dunning Log-Likelihood test, and use a close analogue to the Bonferroni correction Da calls for and then never runs, a Holm-Sidak correction. ^[I am not a statistician, but I use the Sidak correction because the literature seems to say it’s superior to the Bonferroni. I use the Holm modification, which applies increasingly stringent standards as you descend a list, because of an issue Da doesn’t ever address, type II errors; that it is as incorrect to report a false negative as a false positive. I order the Holm method is by word frequency, not p-value (suggested in some online literature) to make the test more conservative; since Jockers and Kiriloff use the 310 most common words, there’s no need to worry about multiple comparisons outside this range.] The result: 81% of the words Jockers and Kiriloff look at are statistically significant.
After spending a paragraph and a half throwing out statistical claims that
My intellectual disagreement, here, is with the
Piper on Confessions
This same slapdash method–mis-stating the statistical or computational literature, failing to run the very tests she insists are necessary, and then leaving the reader with the impression she has somehow invalidated the result–is on prime display in her description of Andrew Piper’s work on the confessional form. Da pulls statistical pronouncements out of thin air and presents them as that which must be done. These claims are often either misinformed or misleading.
I can’t bear to go through all her sections. But as an example, take the analysis of Andrew Piper’s work on Augustine’s Confessions. In a few paragraph, she makes as many mistakes as she holds him to account for in a full article.
First, she criticizes Piper for performing Principal Components Analysis on unscaled word frequencies, and produces scatterplots that show dramatically different results from his: “The way to properly scale this type of matrix is outlined in G. Casella et al’s Introduction to Statistical Learning… The second step [Z-scaling] is necessary if each word is to be seen as a feature for PCA.” George Casella did not write a book called Introduction to Statistical Learning; she means the 2013 volume by Gareth James et al. published (after Casella’s death) in a Springer series for which he was general editor. The chapter she cites certainly does not say that PCA matrices must always be scaled by standard deviations. It says, rather that scaling PCA is a consideration the researcher should take. When units are arbitrary, PCA should be scaled–if comparing SAT scores to grade point averages, you don’t want the difference between a 1420 and a 1421 on the test to be the same as a 2.5 and a 3.5 on the GPA. But word frequencies are not arbitrary. In those cases, the researcher must decide. To quote from the text: “In certain settings, however, the variables may be measured in the same units. In this case, we might not wish to scale the variables to have standard deviation one before performing PCA."@james_introduction_2013.
This is a central challenge familiar to anyone who has tried to grapple with wordcounts. There are so many uncommon words used once or twice in any given text that, when scaling is used, they can completely swamp the repeated words. A variety of solutions are in common use. TF-IDF scaling drops out the most common words while allowing those of medium frequency to shine through; log transformations of various flavors proliferate. Ideally solutions would not be wholly dependent on the parameter space, but the phrasing of the question matters.
Da sidesteps these all these complications for her reqaders by implying the real difference has to do with a philological failing, that Piper doesn’t stem Latin text. This is something a literary audience can understand, and gestures towards a humanistic critique. But comically, her version reproduces many of the same philological failings. She implies that Piper didn’t use a Latin stemming algorithm because the “only Latin stemmer available is the Schinke stemmer,” but that she has taken the effort. This is incorrect on both fronts. First, there are many Latin stemmers available. (For an in-depth analysis of at least 6, see Patrick Burn’s work.
And her effort seems to be scattershot at best. It’s hard to tell
what code Da actually ran–the
online appendices for
analyzing Piper’s case only include the PCA code for Chinese, not the
figures included in the appendix. (Ordinarily I would be forgiving of
this kind of lapse, which is all too common; perhaps the inadequate
code appendices are intended as a higher-order critique of
computational work. But her failings vis-a-vis replication are far
greater than those of, say, Ted Underwood, who generally supplies a
single script called replicate.py that you can run yourself inside
any of his projects.)
Still, from what she has posted online, Da appears to have re-implemented Schinke’s algorithm in both R and python, with separate rules for nouns and verbs. But then, in her Cross Distance code, she simply applies the noun stemming rules to all words, (probably) because choosing a part of speech is much harder than running stemming. This results in many problems; both because some verbs are not stemmed at all (‘resurrexit’ remains ‘resurrexit’ even though the verb rules would have it as ‘resurrexi’); and because the rules are applied to function words as well with silent NULL results in her code, so that words like ‘que,’ ‘cum,’ ‘te,’ and ‘me’ are deleted from the text altogether. That is: many function words are being dropped altogether because a new implementation was hastily coded rather than using one of the more mature implementations available.
I wrote this and then, quickly, checked what difference it all makes. (Code and edits online here) I was, honestly, expecting that the scaling factor would be significant and account for the differences in texts. But actually, what I got looks more or less like Piper’s original.
Reproduction of Piper’s original:
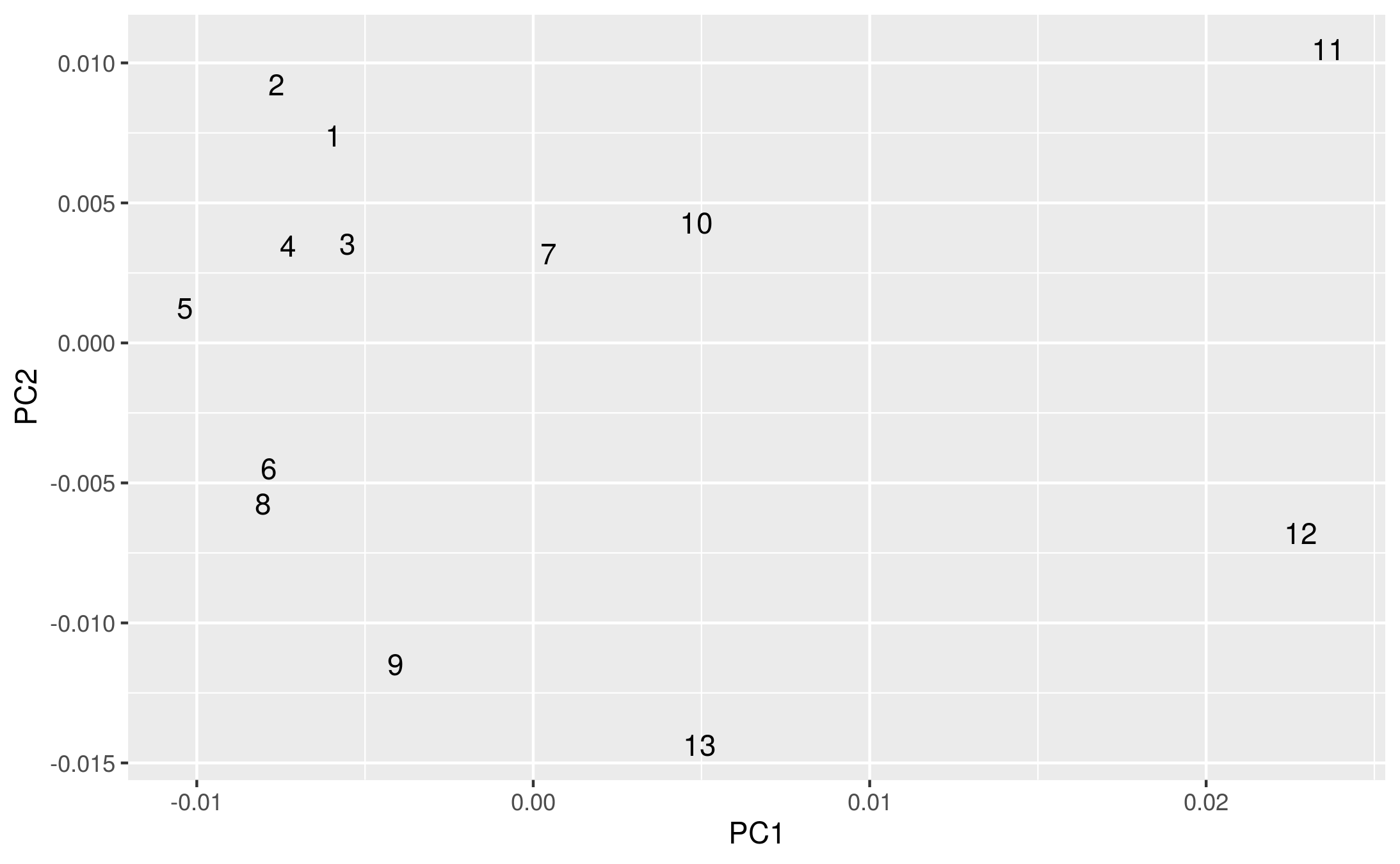
Reproduction using Da’s scaling.
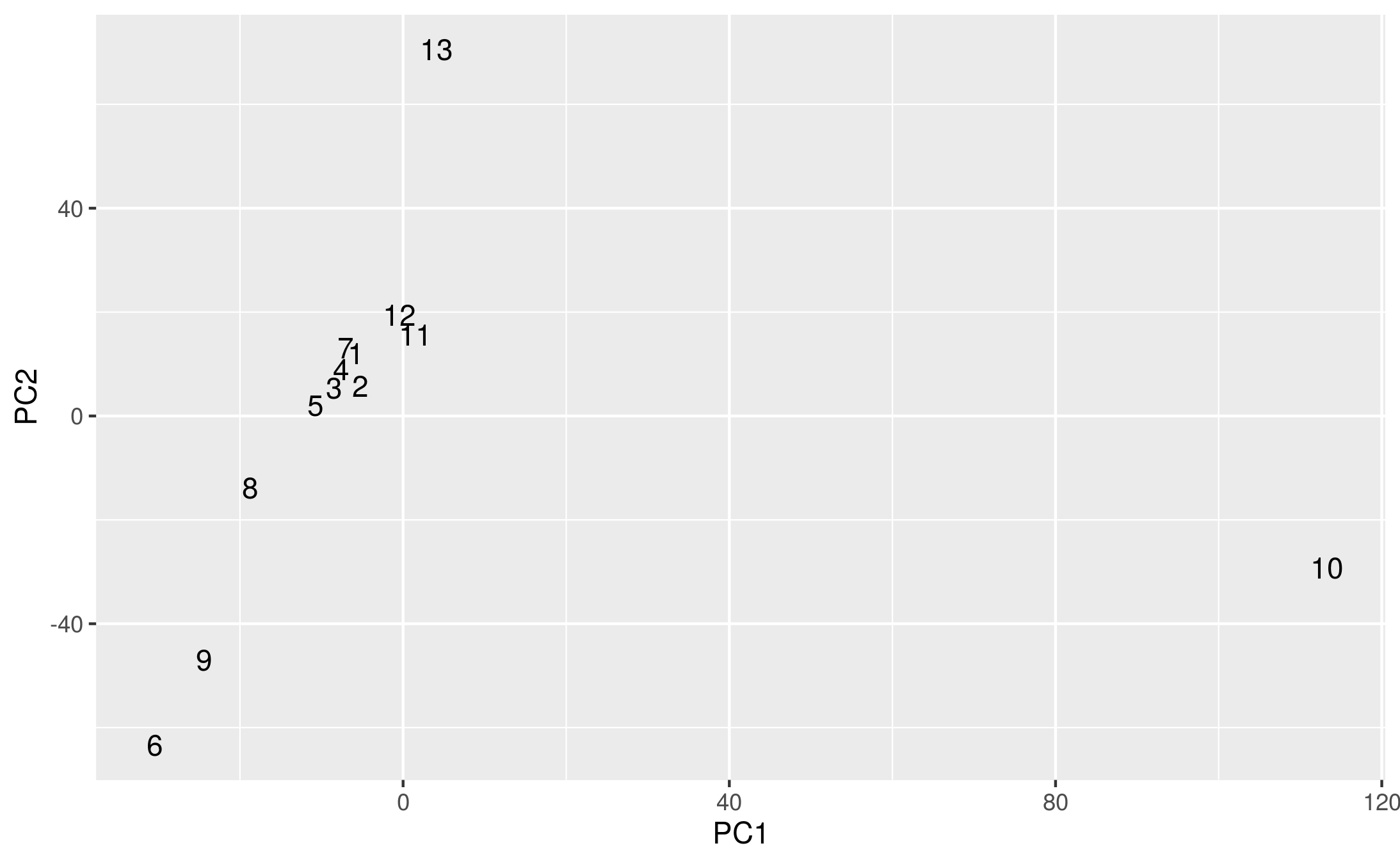
Or maybe it looks completely unlike it!
And so on.
I could go on. The debunking of topic model, for example, uses not the well established literature about comparing topic model distributions to each other, but some arbitrarily chosen robustness tests. (It drops 1% of documents). But it is not a replication. Topic models rely on extremely specific assumptions about the distribution of words in texts based on word counts; they attempt to reproduce the frequencies in actual documents.
But rather than fit on word counts, the model, for no
apparent reason,
uses TF-IDF vectors
that multiply the significance of rare words and decrease the
significance of common ones. I have never seen a TF-IDF vectorization
fed into an LDA feature set before– it’s an extremely odd choice that
guarantees the results will be different from Underwood and
Goldstone’s, and partially explains the incoherent topics in the
appendix, such as doulce attractiveness unsatisfying gence dater following mecum wigan cio milieu.
In fact, Goldstone and Underwood’s original work on this dealt with this issue very clearly:
On the other hand, to say that two models “look substantially different” isn’t to say that they’re incompatible. A jigsaw puzzle cut into 100 pieces looks different from one with 150 pieces. If you examine them piece by piece, no two pieces are the same — but once you put them together you’re looking at the same picture.
This comparison obviously mislabels its bins (it claims that her replication found the “she killed” and “he wept” are gender stereotypes, rather than the opposite) and makes some extremely fishy claims such as “Overall, the percentage differences between these top most correlated verbs for each gender was very low (0.031% to 0.307%) meaning that while a difference can be found, male/female is not very differentiated from one another if we look at verbs.” I don’t know what that range is supposed to be, but at least for ‘wept’, Google Ngrams gives the difference in gender usage as 400%
But to go through all of this is a pain. I’m sure others have written other analyses. This work is tedious, which is the reason that it’s rarely done; and it’s hard to reproduce another workflow even when it’s well-documented.
-
Nearest shrunken centroids is indeed a sort of idiosyncratic choice, but one that Jockers seems to be extremely partial to going back over a decade. @jockers_comparative_2008. Whether digital humanists should be free to roam across the disciplines in search of obscure but useful algorithms, or should remain in a tightly constrained space, is a difficult one. My stance– ↩︎